通解公式,伯努利方程通解公式什么样？

p+1/2ρv2+ρgh=C。 伯努利原理往往被表述为p+1/2ρv2+ρgh=C，这个式子被称为伯努利方程。式中p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，C是一个常量。它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。 需要注意的是，由于伯努利方程是由机械能守恒推导出的，所以它仅适用于粘度可以忽略通解公式、不可被压缩的理想流体。

举一个简单的例子：

y/’/’+3y/’+2y = 1 (1)

其对应的齐次方程的特征方程为：

s^2+3s+2=0 (2)

因式分 (s+1)(s+2)=0 (3)

两个根为： s1=-1 s2=-2 (4)

齐次方程的通

y1=ae^(-x)+be^(-2x) (5)

非奇方程(1)的特

y* = 1/2 (6)

于是（1）的通解为：

y=y1+y* = 1/2 + ae^(-x) +be^(-2x) (7)

其中：a、b由初始条件确定.

公式是∫e^(-p(x))dx，这个积分是个不定积分，本身就包含了一个常数。不用再写∫e^(-p(x))dx+c了。

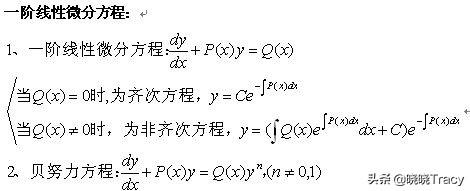
扩张资料

什么叫做一阶线性微分方程？

形如(记为式1)的方程称为一阶线性微分方程。其特点是它关于未知函数y及其一阶导数是一次方程。这里假设,是x的连续函数。

若,式1变为(记为式2)称为一阶齐次线性方程。 如果不恒为0,式1称为一阶非齐次线性方程,式2也称为对应于式1的齐次线性方程。 式2是变量分离方程,它的通解为,这里C是任意常数。

正常情况下，微分方程方程都有边界条件和/或初始条件，当你知道p(x)的具体形式时，算这个不定积分，应该保留一个常数，而后用边界条件和/或初始条件来确定常数的值，得到完全确定的解。