matlab编程实例100篇,怎么在MATLAB里面找例子?
1matlab编程实例100篇、实现方法
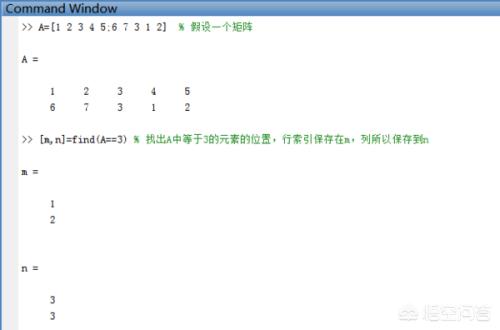
使用find()函数:[m,n]=find(A==x)
2、解析
A==x:将矩阵A的每个元素与x比较,如果相等,相应位置的元素就等于1,否则为0。
find(X):返回X中非零元素的索引(即行列位置)。
3、实例演示:找出矩阵A中所有等于3的元素的行列位置
打开matlab,在命令窗口运行如下代码:
>>A=[12345;67312]
>>[m,n]=find(A==3)
从运行结果可知,找到A中元素3的位置为:第1行第3列和第2行第3列。
求一个matlab的程序
clearclc;n=100;t=0:pi/n:2*pi;xo=cos(t);yo=sin(t);%big circlek=0;[m,n]=size(xo);for i=1:n xi=xo(i)+0.05.*cos(t);%little circle yi=yo(i)+0.05.*sin(t); fill(xi,yi,’r’);hold onplot(xo,yo);axis([-1.2 1.2 -1.2 1.2])% axis equaldrawnowhold offpause(0.01)%M(:,:,i)=getframe;end %movie(M,2,2)
帮忙写个Matlab小程序
我们学校的数学建模上机课也有Mathlab程序,看看下面有没有你要找的。
一 基本运算
1 求
输入(12+2*(7-4))/3^2执行
2 输入x = (5*2+1.3-0.8)*10^2/25执行
再输入y= 2*x+1执行
3 执行clear命令。观察结果
4计算圆面积Area = ,半径r = 2,则可键入
r=2;area=pi*r^2; area
问:语句末尾加分号与不加分号有何区别?请试验之
5常用函数
名称 含义 名称 含义
sin 正弦 exp E为底的指数
cos 余弦 log 自然对数
tan 正切 log10 10为底的对数
cot 余切 log2 2为底的对数
asin 反正弦 abs 绝对值
acos 反余弦
例:1)执行y = sin(10)*exp(-0.3*4^2)
2) 想计算 的值
输入y1=2*sin(0.3*pi)/(1+sqrt(5))执行之
若又想计算 ,可以简便地用操作:先按á键则会出现上面输入过的指令 y1=2*sin(0.3*pi)/(1+sqrt(5)) ;然后移动光标,把y1改成y2;把 sin 改成 cos 便可。即得
y2=2*cos(0.3*pi)/(1+sqrt(5))然后执行之。
系统默认4位有效数字,若想提高精度则可如下:
digits(10);sym(y2,’d’) 执行就可精确到小数点后10位,还可将10改为其它数字试验
二 矩阵运算
1要得到矩阵 ,
可输入A = [1,2,3; 4,5,6; 7,8,9] 执行,观察结果
还可分行输入
A=[1,2,3
4,5,6
7,8,9]
效果相同
2 注意 %号后的语句为注释,练习时不必输入
>>a=[1,4,6,8,10] %一维矩阵
>>a(3) % a的第三个元素
ans =
6
»x =[1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 11]; %二维2×8 矩阵
执行后双击左边Workspace里的x,观察之
» x(3) % x的第三个元素
ans =
2
» x([1 2 5]) % x的第一、二、五个元素
ans =
1 4 3
如需要还可定义b=x([1 2 5])执行后结果为
b =
1 4 3
>> x(2,3) % x的第二行第三列的元素
ans =
6
x(1:5) % x的第前五个元素
ans =
1 4 2 5 3
» x(10:end) % x的第十个元素后的元素
ans =
8 6 9 7 10 8 11
执行后双击左边Workspace里的x,观察是哪十个元素
» x(10:-1:2) % x的第十个元素和第二个元素的倒排
ans =
8 5 7 4 6 3 5 2 4
» x(find(x>5)) % x中大于5的元素
ans =
6 7 8 6 9 7 10 8 11
» x(4)=100 %给x的第四个元素重新给值
x =
1 2 3 4 5 6 7 8
4 100 6 7 8 9 10 11
» x(3)=[] % 删除第三个元素(不是二维数组)
x =
Columns 1 through 12
1 4 100 3 6 4 7 5 8 6 9 7
Columns 13 through 15
10 8 11
» x(16)=1 % 加入第十六个元素
x =
Columns 1 through 12
1 4 100 3 6 4 7 5 8 6 9 7
Columns 13 through 16
10 8 11 1
3 如不需要以前的变量时,为不干扰以后计算,可执行clear清除以前的变量
当元素很多的时候,则须采用以下的方式:
» x=(1:2:121); % 以起始值为1,增量值为2,终止值为121的矩阵
» x=linspace(0,1,100); % 利用linspace,生成以0为起始值,1为终止值,元素数目为100的矩阵
»a=[] %空矩阵
a =
[]
» zeros(2,2) %全为0的矩阵
ans =
0 0
0 0
» ones(3,3) %全为1的矩阵
ans =
1 1 1
1 1 1
1 1 1
» rand(2,4); %随机矩阵
4另外一种定义矩阵的方式
»a=1:7; b=11:2:23;
»c=[b a]; %利用上面建立的阵列 a 及阵列 b ,组成新阵列c
»d=[b ; a]; %利用a及b,组成新矩阵d
执行后双击左边Workspace里的c与d,比较之
再如 已知y=[-1,6,15,7,31,2,4,5];
x=y(3:5) %x为y的第三到第五个元素组成的新向量
或 x=[y(5),y(3),y(7)] %x为y的第五、第三、第七个元素组成的新向量
或这样更简单 x=y([5,3,7])
5 输入矩阵x=[4,8,12,10,23;6,3,15,13,19;9,1,2,18,14;11,7,5,21,17]
依次输入下列命令并执行,观察结果,各命令分别有什么作用?
max(x)
min(x) (问:如何得到整个矩阵的最小值与最大值?)
[m,n]=size(x)
L=length(x)
y=x’
a=x( :,2)
b=x( :,2)’
c=x(3,
















