sin120°等于多少（石材行业常用的几个数学公式，你都会吗）

点一下掌握：有石CAD，石材提交订单排版设计就这么简单

欢迎大家检索关心《石材研习社》微信公众平台，点击查看石材文章内容

数学课做为处理各种各样课程的前提而关键的一种手段和人类工作和生活息息相关，已经渗入人类工作和生活的各个领域，离开数学课大家无法想象人类工作和生活会错乱到怎么样的水平，算得上是“举步维艰”，数学课在人类工作和生活中肩负着重要作用。同样，石材产品生产加工中自然少不了运用数学的知识和基本定理去解决生产制造加工中的一些问题，减少了这些内容和基本定理大家是没有办法搞好商品加工工作的。石材产品加工中到底有哪些数学思想方法和基本定理石材是作为工作人员必须了解和娴熟运用的呢？

#1

勾股定理

这一定律是石材产品加工处于第一位的，也是不可少。

勾股定理关系式：c2=a2 b2

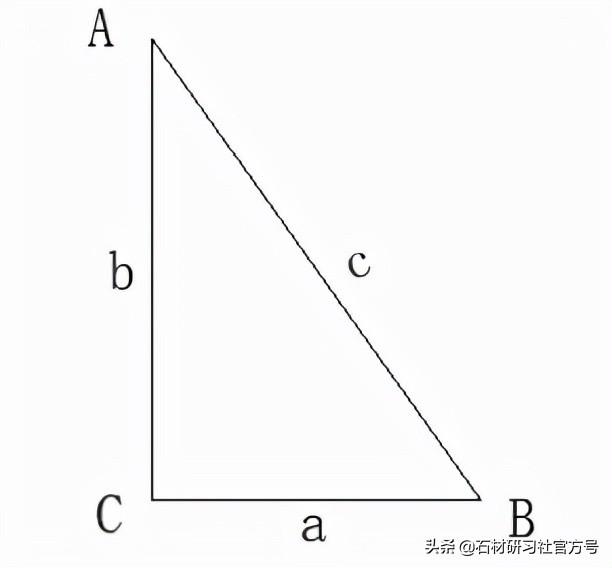
图1

石材产品加工中常见勾股定理测算矩形板的对角。如切一件长短1000mm，总宽800mm的矩形板，根据勾股定理获得对角线长度为

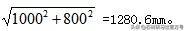
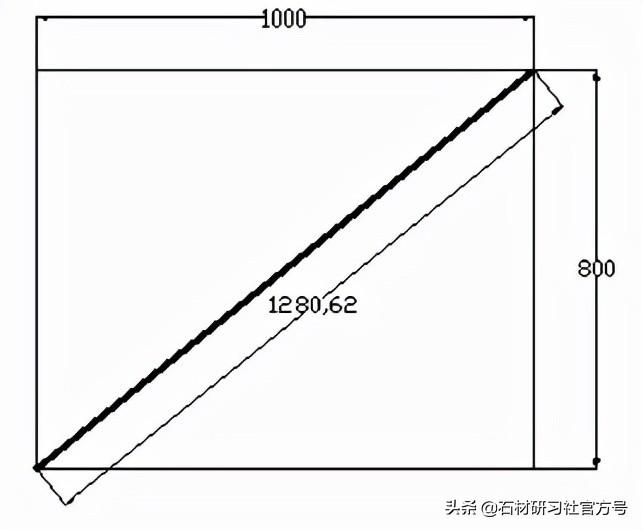
图2

#2

三角函数的常用公式

SinA=a/c，sinB=b/c，tgA=a/b，ctgA=b/a 。tgA *ctgA=1。

c为直角三角形斜度，a为与∠A相对应的边，b为∠A邻近的边。

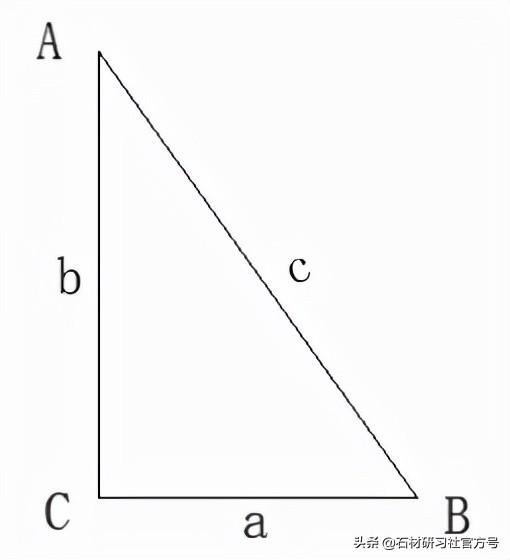
图3

#3

弦长、圆心角计算方法

弦长B=2Rsinθ/2。（θ为圆心角，R为圆半径）。

θ=2arcsinB/2R。

这一计算公式圆弧板弦长、圆弧状异型板极为有效。记住并且还会运用后，一般的生产员工都是会自身测算了。

倘若生产制造加工圆心角θ=60°，半经R500的扇型板，需要下什么尺寸块料才能够加工工程图4的商品。

根据公式计算弦长

B=2Rsinθ/2=2*500*sin(60°/2)=1000*sin30°=1000*1/2=500。

因而开料规格不可以低于500mm*500mm。

记牢好多个常见角度三角函值，石材产品加工中这些视角极其普遍。

Sin60°=sin120°=√3/2=0.866；Sin30°=sin150°=1/2；Sin45°=sin135°=√2/2=0.707；Sin90°=1；

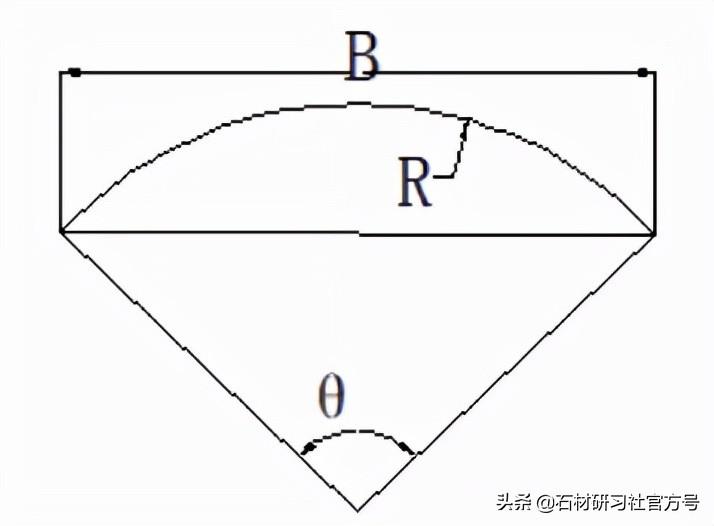
图4

#4

余弦定理

余弦定理关系式：c2=a2 b2-2abcosC

有些客户要加工一件周长为800、900，600的三角形板，制做这类异型板生产员工就需要算出三角形A、B、C中两个角方可加工出这类异型板。

运用余弦定理各自算出三角形的A、B、C三个角。

不受影响数值，能够假设a=800，b=900、c=600。

6002=8002 9002-2*800*900cosC，从而得cosC=0.7569，C=41°；

9002=8002 6002-2*800*600cosB，从而得cosB=0.1979，B=78.6°；

求A角运用三角形三个角总和为180°测算，

A=180°-78.6°-41°=60.4°。

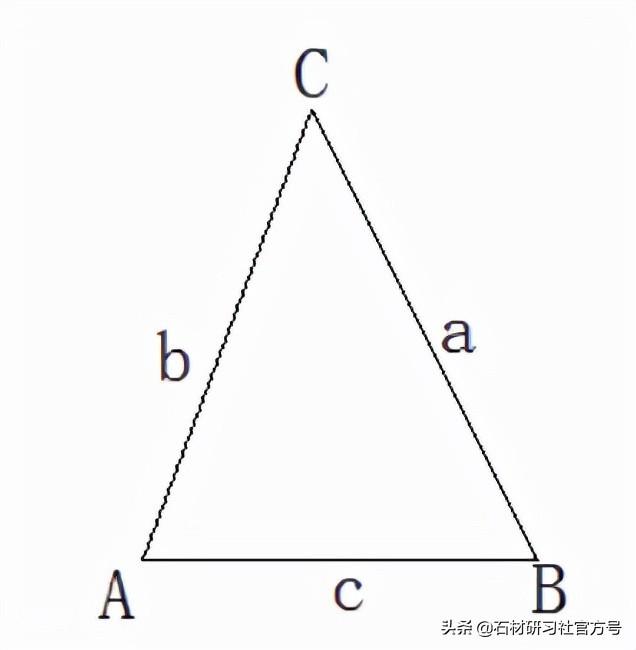
图5

图4中假如加工的并不是扇型板，是弧形板，下多块料才能够加工出这一件弧形板呢？

弧形的拱高=R-Rcosθ/2=500-500cos30°=67，因而加工图4弧形板最少切料规格为500*67。

#5

正弦定理

a/sinA=b/sinB=c/sinC=2R。

以上边的事例，用正弦定理求得三角形角度。

首先用余弦定理求角三角形的一个视角，再换正弦定理求得其他2个视角。

上边事例占用余弦定理求取C夹角41°，再换正弦定理求A有、B角。

800/sinA=600/sin41°，

sinA=800*sin41°/600,sinA=0.8747,A=61°；

900/sinB=600/sin41°，sinB=900*sin41°/600，sinB=0.98，B=78.5°。

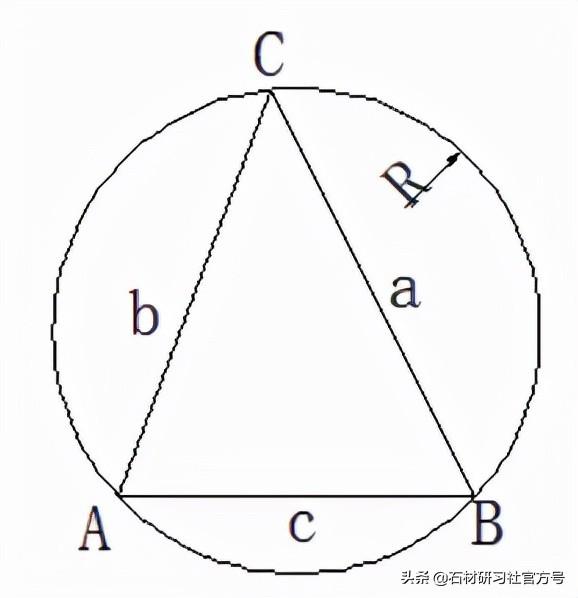
图6

这个时代专业知识的年代，掌握一些数学思想方法看起来用不着，事实上是很有必要的，由于数学的作用是非常大的，已经深层次到这个整个社会各个方面，对生活与工作有很大的功效。原文中所介绍说的勾股定理虽经历了数千年，但一直是学习数学必学的基本定理，如果没有它几何图形中的很多问题也解决不了，生产制造实际操作中的诸多问题测算难以实现。

期待这些公式对石材的生产员工有非常大的协助，在今后的工作中碰到相似的测算无需托人了。

创作者 | 晏辉

未授权切勿转截