降幂公式

升幂和降幂本身并没有意义，只有当指定按照某个字母或者某个数的升降幂排列才有意义按照某个字母数的升幂降幂排列是指按照该字母数的次幂从高次幂到低次幂从低次幂到高次幂排列，不含该字母数。

即cossincos222另外，由2cos1cos22可得2cos1cos22从而1cos2cos22同12sincos2样2sin21cos2212sin1cos222sincossin21sincossin2222cos1cos212cos1cos2222sin1cos212sin1cos22降幂升角公式1求。

三角函数的降幂公式 sin#178α=1cos2α2 cos#178α=1+cos2α2 tan#178α=1cos2α1+cos2α三角函数降幂公式推导过程 运用二倍角公式就是升幂，将公式cos2α变形后可得到降幂公式。

在数学学习中，很多同学不明白什么是降幂，怎么进行降幂运算，本文收录了部分降幂公式，帮助同学更好地解决难题降幂公式，其实就是降低指数幂由2次变为1次的公式，可以减轻二次方的麻烦。

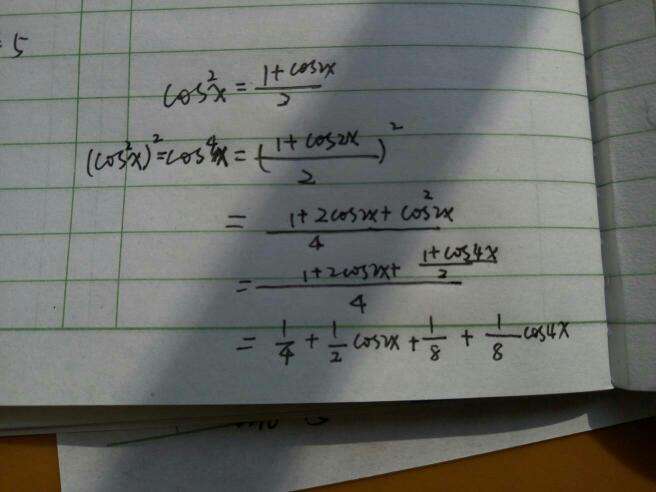
三角函数降幂公式 三角函数的降幂公式是cos#178α = 1+ cos2α 2 sin#178α=1cos2α 2 tan#178α=1cos2α1+cos2α运用二倍角公式就是升幂，将公式cos2α变形后可得到降幂。

三角函数的降幂公式是cos#178α = 1+ cos2α 2 sin#178α= 1 cos2α 2 tan#178α=1cos2α1+cos2α 发展历史 起源 公元五世纪到十二世纪，印度数学家对三角学作出了较。