正弦定理证明

证明连接AD，因为DC是圆O的直径半径为R，所以角DAC=90度，所以三角形DAC是直角三角形，所以sin角ADC=ACDC=AC2R因为角B=角ADC，所以ACsinB=2R，同理可证ABsinC=BCsinA=2R，所以正弦定理BCsinA。

正弦定理是三角学中的一个基本定理，它指出“在任意一个平面三角形中，各边和它所对角的正弦值的比相等且等于外接圆的直径”，即asinA=bsinB=csinC= 2r=Dr为外接圆半径，D为直径正弦定理的证明方法 正弦。

在解三角形中，有以下的应用领域已知三角形的两角与一边，解三角形已知三角形的两边和其中一边所对的角，解三角形运用abc=sinAsinBsinC解决角之间的转换关系高中数学正弦定理公式之定理证明 外接圆证明正弦定理。

证明如下在三角形的外接圆里证明用BC边和经过B的直径BD，构成的直角三角形DBC可以得到2RsinD=BCR为三角形外接圆半径角A=角D得到2RsinA=BC同理2RsinB=AC，2RsinC=AB这样就得到正弦定理了正弦。

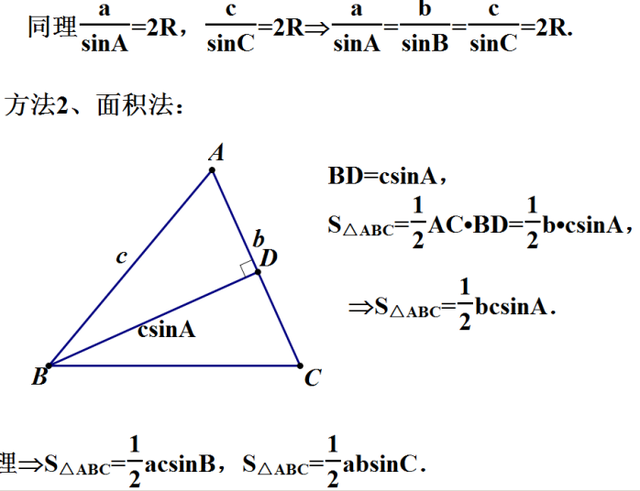
正弦定理三角形ABC中 BCsinA=ACsinB=ABsinC 证明如下在三角形的外接圆里证明会比较方便 例如，用BC边和经过B的直径BD，构成的直角三角形DBC可以得到2RsinD=BC R为三角形外接圆半径角A=角D 得到2RsinA=B。