什么是勾股定理和毕达哥拉斯定理 两者在数学里面的应用有哪些

勾股定理是指在直角三角形中，直角边的平方等于另外两条边的平方和。毕达哥拉斯定理是指在直角三角形中，斜边的平方等于直角边的平方和。它们可以用来求解直角三角形的各种问题，例如求解三角形的面积、周长、角度等。还可以用来解决一些几何问题，例如求解圆的直径、正方形的对角线等。因此学习和掌握这两个定理对于数学学习和应用都非常重要。

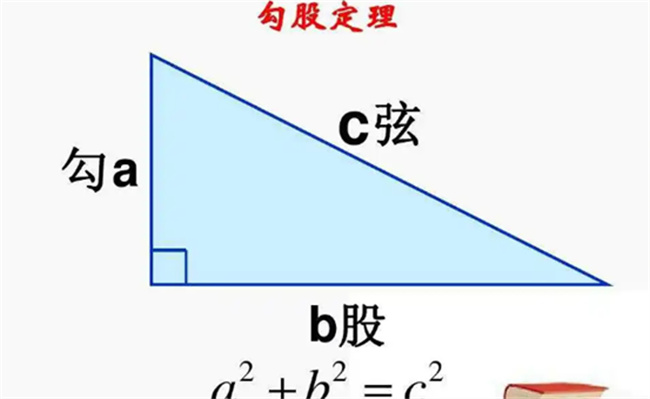
设直角三角形的两条直角边分别为a和b，斜边为c，则有：a² + b² = c²，这就是勾股定理。证明方法如下：假设有一个直角三角形，其直角边分别为a和b，斜边为c。将这个三角形的两个直角边分别平移一段距离，使它们相邻并且与斜边垂直。

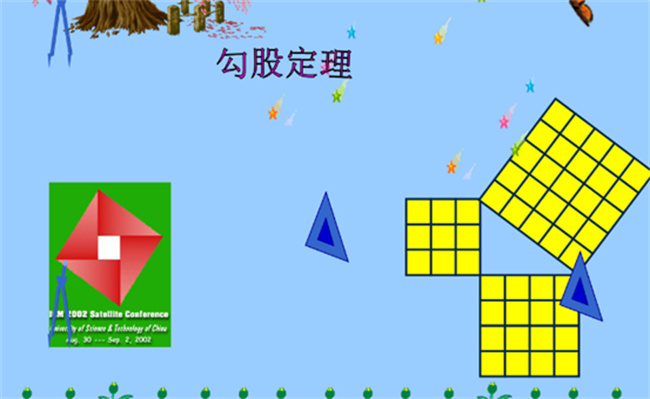
由于这两个直角边与斜边垂直，所以它们的长度可以表示为斜边长度的一部分。设它们的长度分别为x和y，则有：a = c * sinθ = c * y / c = y，b = c * cosθ = c * x / c = x，根据勾股定理，有：a² + b² = c²，代入上面的式子，得到：x² + y² = c²，这就证明了勾股定理。

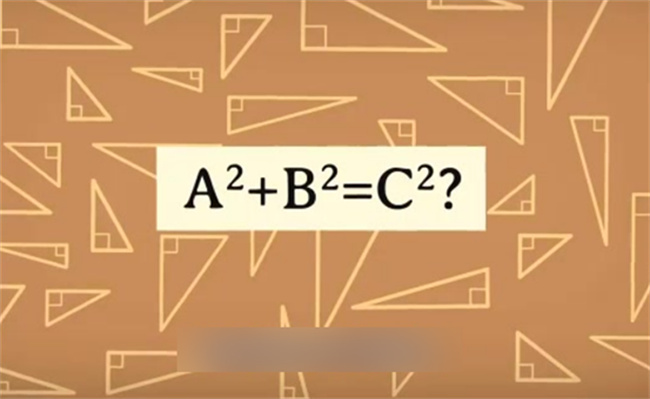
毕达哥拉斯定理设直角三角形的两条直角边分别为a和b，斜边为c，则有：c² = a² + b²，证明方法如下：假设有一个直角三角形，其直角边分别为a和b，斜边为c。将这个三角形的两个直角边分别平移一段距离，使它们相邻并且与斜边垂直。由于这两个直角边与斜边垂直，所以它们的长度可以表示为斜边长度的一部分。设它们的长度分别为x和y，则有：a = c * sinθ = c * y / c = y，b = c * cosθ = c * x / c = x根据勾股定理，有：a² + b² = c²，代入上面的式子，得到：x² + y² = c²，这就证明了毕达哥拉斯定理。