什么是正弦定理证明常用哪4种方法

摘要正弦定理是在三角形ABC中，已知三边a、b、c和其中一个角A（角A必须是非直角角度），求角A所对边a的长度的定理。其公式表达式为：a/sinA = b/sinb = c/sinC，其中sinA表示角A的正弦值，a表示角A所对边的长度，B、C与b、c的含义同理。可以利用正弦定理的定义推导、利用三角形面积公式推导、利用海伦公式推导、利用欧几里得法证明等。利用正弦定理的定义推导：对于任意的三角形ABC，

正弦定理是在三角形ABC中，已知三边a、b、c和其中一个角A（角A必须是非直角角度），求角A所对边a的长度的定理。其公式表达式为：a/sinA = b/sinb = c/sinC，其中sinA表示角A的正弦值，a表示角A所对边的长度，B、C与b、c的含义同理。可以利用正弦定理的定义推导、利用三角形面积公式推导、利用海伦公式推导、利用欧几里得法证明等。

利用正弦定理的定义推导：对于任意的三角形ABC，都满足以下关系：a/sinA = b/sinB = c/sinC。

对于三角形ABC中的任何一个非直角角度A：sinA = a/b * sinB = a/c * sinC，这就是正弦定理的证明。利用欧几里得法证明：对于任何平面三角形ABC，再单独考虑其中的某一个角A。假设其高H与BC相交的点为D，则有：BD/AH = c/b，AD/AH = sinB，AD/BD = AC/BC = sinA/sinB，将上式组合起来，可以得到正弦定理的形式：a/sinA= b/sinb = c/sinC。

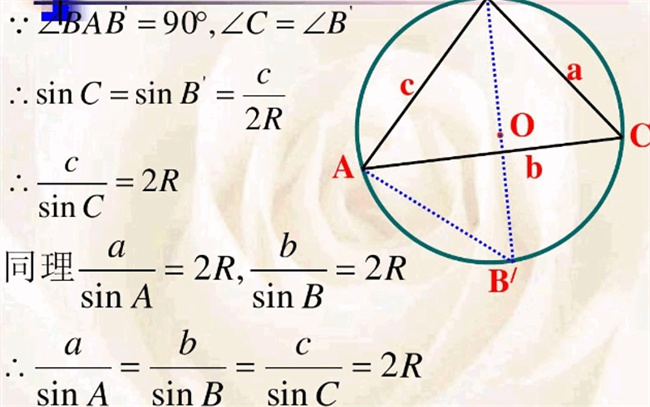
利用三角形面积公式推导：根据向量叉积的定义，假设三角形ABC的两个向量分别为$\vec{a}$=(x1,y1,z1), $\vec{b}$=(x2,y2,z2)，其叉积表示为$\vec{a}$ × $\vec{b}$ = $\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \ x_1 & y_1 & z_1 \ x_2 & y_2 & z_2 \end{vmatrix}$，可以得到三角形ABC面积的公式为：S = 1/2 |$\vec{a}$ × $\vec{b}$|，对于三角形ABC中的任何一个非直角角度A，可以将其面积分别表示为：S = 1/2 * a * b * sinC = 1/2 * a * c * sinB

将上式两边除以a，再变形，可以得到正弦定理的形式：a/sinA= b/sinb = c/sinC。

利用海伦公式推导：对于三角形ABC，假设其三边长为a、b、c，海伦半周长为p，即：p = (a+b+c)/2，则三角形ABC的面积可以表示为：S = √p(p-a)(p-b)(p-c)，对于三角形ABC中的任何一个非直角角度A，可以将其面积表示为：S = 1/2 * a * b * sinC = 1/2 * b * c * sinA，将上式两边除以bc，并将海伦公式代入，可以得到正弦定理的形式：a/sinA= b/sinb = c/sinC。